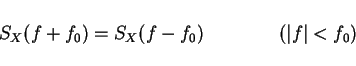Next: About this document ...
Up: Random Processes II
Previous: GAUSSIAN PROCESSES
Must work about these for multiplying many signals using same channel (like radio)
Now need to worry about decomposition
Any X(t) can be decomposed into its sin portion and its cosine portion. What we
want to do is represent X(t) as a modulated signal
The Xc(t) and Xs(t) are "baseband" processes
Hilbert tells us
FALLOUT
Thm.
X(t) is a stationary BP process (BW=2W)
 and Xc(t) are jointly stationary lowpass (baseband) processes each having the power of X(t)
and Xc(t) are jointly stationary lowpass (baseband) processes each having the power of X(t)
BP
Since SX(f) limited to |f-f0|<W then
SXc/s(f) limited to |f|<W
same idea (notice
SXs Xc(0)= always)
Important
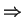 if X(t) is such that
if X(t) is such that
then cross corr is zero!
i.e.
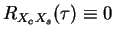 everywhere!
everywhere!
So, say X(t) is also zero mean
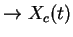 and Xs(t) also zero mean (easy to see)
and Xs(t) also zero mean (easy to see)
Therefore, Xc(t) and Xs(t) uncorrelated
Say X(t) is also gaussian
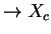 and Xs jointly gaussian
and Xs jointly gaussian
Therefore, Xc and Xs INDEPT
FINALLY,
PX=RX(0)=RXc(0)=RXs(0)
Powers in Xc(t) nd Xs(t) same as in X(t)
END



Next: About this document ...
Up: Random Processes II
Previous: GAUSSIAN PROCESSES
1999-02-06
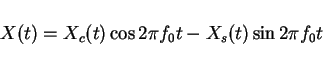
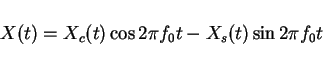
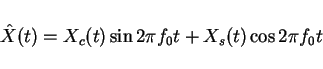
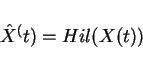
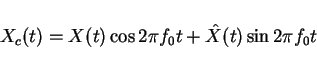
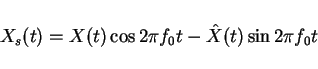
![]() and Xc(t) are jointly stationary lowpass (baseband) processes each having the power of X(t)
and Xc(t) are jointly stationary lowpass (baseband) processes each having the power of X(t)
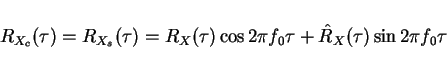
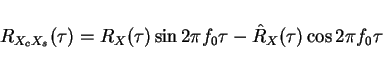
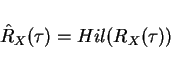
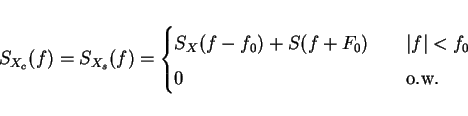
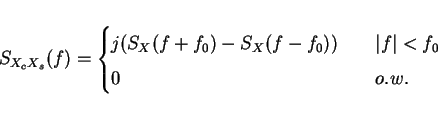
![]() if X(t) is such that
if X(t) is such that