GAUSSIAN PROCESSES

Def.
X(t) gaussian if X(t₁),X(t₂),... jointly gaussian RV's
Mean and covariance matrix completely specify joint distribution so
Thm.
A gaussian process is COMPLETELY characterized by R_X(t₁,t₂) and m_X(t)pf. Remember, cov(X,Y)=E(XY)-E(X)E(Y)         (x,y real)

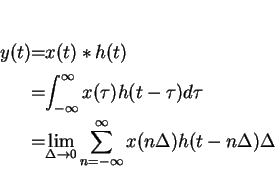
By Thm
pf. LTI has

$$\begin{eqnarray*}y(t)&=&x(t)*h(t)\\ &=&\int_{-\infty}^{\infty}x(\tau)h(t-\tau)d... ...arrow 0}\sum_{n=-\infty}^{\infty} x(n\Delta) h(t-n\Delta) \Delta \end{eqnarray*}$$

ie.each y(t) is a linear/superposition of joint gaussians. Therefore, any set of y(t_i) are jointly gaussian (see pp.159 text)
Which is why everybody always beats you up w/ Gaussians

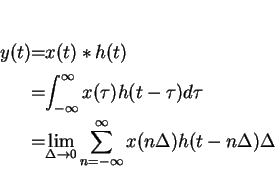
Thm
If gaussian WSS $\rightarrow$ SSS
pf. Gaussian process is completely characterized by its mean and autocov.

Thm
Useful Stuff. If

$$\int_{-\infty}^{\infty}\left\vert R_X(\tau)\right\vert d\tau<\infty$$

and X(t) gaussian w/ m_X(t)=0
Then X(t) stationary. (read tje pf. LONG AGO but don't remember the time)

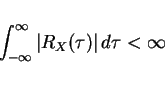
Joint Gauss Process
X(t),Y(t) are jointly gauss if X(t₁)...X(t_n) Y(t₁)...Y(t_n) are jointly gaussian.
Thm.
If X(t) and Y(t) jointly gaussian then uncorrelated $\Rightarrow$ indept.
pf. Covariance matrix has no diag. terms so determinent is product of diag terms and

$$e^{x^TC x/2}=\Pi_{i=1}^N e^{x_i^2/2 C_{ii}^2}$$

i.e. the joint distribution becomes a product dist.

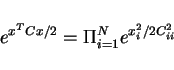
WHITE Process

Def.
S_X(f)= const. $\Rightarrow X(t)$ is white (allcolor spectrum)
so $R_X(\tau)=$ const $\delta(\tau)$
$\Rightarrow$ IMPORTANT X(t₁) X(t₂) UNCORRELATED if $t_1\ne t_2$
If gaussian process $\rightarrow X(t_1)$ indept.X(t₂)

Noise and LTI

S_Wc(f)=S_W(f)|H(f)|²=N₀|H(f)|²

Noise equivalent BW
(Don't like this but it is a common def. and manufacturers like it)

1.

Look at |H(f)|² (lets assume its a BP filter)

2.

Find max |H(f)|² at f=f^*

$$B_{neq}=\int_{-\infty}^{\infty}\vert H(f)\vert^2df/2\vert H(f^*)\vert^2$$

3.

Power in output N₀ B_neq |H(f^*)|²
i.e. if they give you B_neq+|H(f^*)| you don't have to do the integral (because they did it for you)

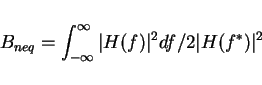
Thm.
Nyquist sampling holds for random processes
i.e. the expected difference between X(t) and $\hat{X}(t)$=reconstruction from samples

$$\begin{eqnarray*}\hat{X}(t)&=&\mbox{LPF} (\sum_n X(nT)\delta(t-nT))\\ &=&\sum_n X(nT)sinc(2W(T-NT)) \end{eqnarray*}$$

is zero if $T_s\le \frac{1}{2W}$
HOWEVER can't say $\hat{X}^(t)=X(t)$ MS not pointwise

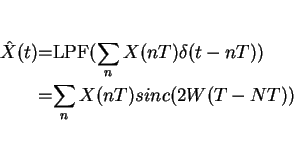
Real Interesting Theorem
If S_X(f) flat over passband, then X(nT) are uncorrelated
I think we should try to prove this same time (think about it).
$\Rightarrow$ Kind of tells you how long you need to want before you get new information.