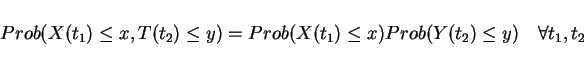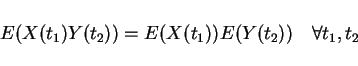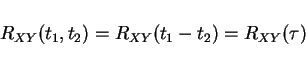Def
Statistics of a Random Process x(t) is the set of joint distributions on (t1,t2,...tn) for any n>0 and any values of
fX(t1)X(t2)...X(tN)(x(t1)...x(tN)) for any n>0 and
Def
mth order statistics
Each w gives a function. Random only because we don't know w ahead of time.
View
x(t) random waveform
x(t1),x(t2) random variables
x(t,w) deterministic waveform
x(t,w) constant
Some definitions
Def
Statistics of a Random Process x(t) is the set of joint distributions on
(t1,t2,...tn) for any n>0 and any values of ![]() ,
i.e. we have available
,
i.e. we have available
fX(t1)X(t2)...X(tN)(x(t1)...x(tN)) for any n>0 and
![]()
Def
mth order statistics
![]() we only know up to joint distribution or M instancesa. We sing and dance when m=2 (gaussian random process has this property that it is completely described by m=2 order stats)
we only know up to joint distribution or M instancesa. We sing and dance when m=2 (gaussian random process has this property that it is completely described by m=2 order stats)
Def Mean
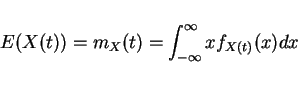
Def Autocorr
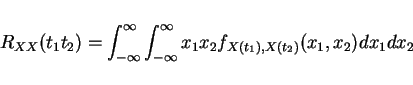
Def Autocov
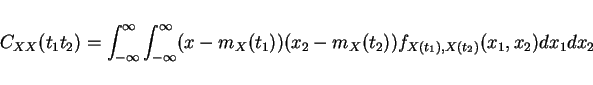
Stationarity
Def Strict sense stationarity (SSS)
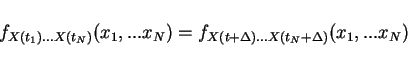
Def Wide sense stationarity (WSS)
mX(t) = constant
![]() only time difference matters
only time difference matters
(![]() for short)
for short)
Def Cyclostationarity
mX(t)=mX(t+kT) for some ![]()
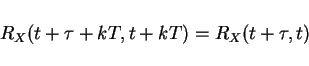
Autocorr of Stationary Process
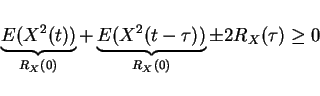
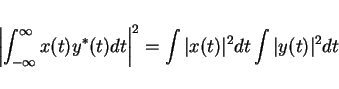
Ergodicity
(Strictly stationary) (simple argument)
Define averages first
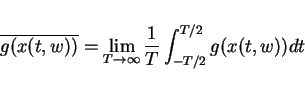
Power and Energy (general)
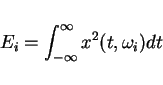
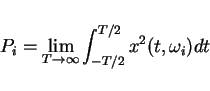
Def PX,EX random variables
CDFs:

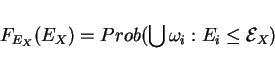
Def
![]()
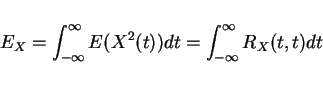
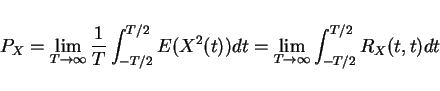
Stationary
![]()
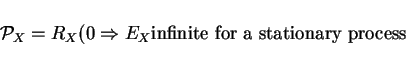
Def