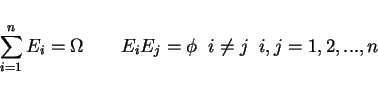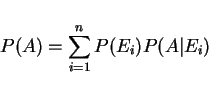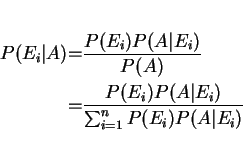Next: Random Variables
Up: Random Processes I
Previous: Random Processes I
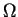 sample space
sample space
Machinery
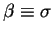 - field on
- field on 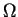
(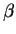 is a subset of
is a subset of 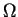 and has special properties)
and has special properties)
Set Defs
-
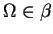
- if event
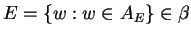 then so is
then so is
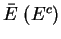
AE is event set
- if
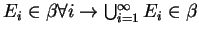
Measure Defs
Probability measure P
- 1.
-
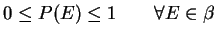
- 2.
-
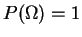
- 3.
- With
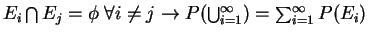
ie. probs. of disjoint events add
Fallout
- 1.
-
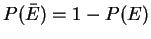
- 2.
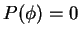
- 3.
-
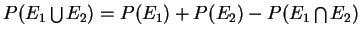
growup notation
P(E1 + E2)=P(E1)+P(E2)-P(E1E2) - 4.
- if
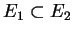 then
then
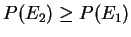
conditional prob
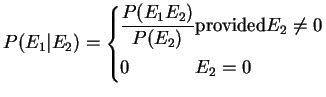
If E1 and E2 indept. above implies
P(E1 E2)=P(E1)P(E2)
Partition
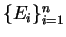 is a finite partition of sample space
is a finite partition of sample space
can project on outcome A onto Ei!
known as total probability theorem, which leads to
which is known as Bayes Thm.
1999-02-06
![]() - field on
- field on ![]()
![]() is a subset of
is a subset of ![]() and has special properties)
and has special properties)
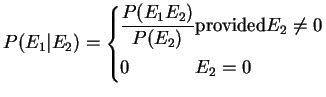
![]() is a finite partition of sample space
is a finite partition of sample space