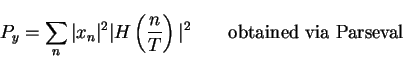define
![]()
![\begin{displaymath}y(t)=T[x(t)]=T[\sum_k x_k e^{j \omega_0 kt}] = \sum_k x_k T[e^{j\omega_0 kt}]
\end{displaymath}](img65.gif)
![\begin{displaymath}T[e^{j\omega_0 kt}]=\int_{-\infty}^{\infty} h(\tau)e^{j\omega_0 k(t-\tau)} d\tau
=e^{j\omega_0 kt} H(\frac{k}{T})
\end{displaymath}](img66.gif)
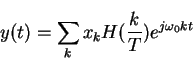
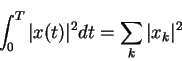
i.e. energy in a period
![]() add up energy in spectral components
add up energy in spectral components
Just spread period out:
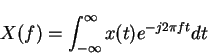
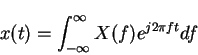
Look! no ![]() and integrals have
f not
and integrals have
f not
![]() .
This is the FT pair - f(t) must satisfy Dirichlet
.
This is the FT pair - f(t) must satisfy Dirichlet
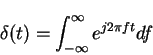
![\begin{displaymath}F[x(at)]=\frac{1}{\vert a\vert}X(\frac{f}{a}) \mbox{\qquad} a\ne0 \quad\mbox{and real}
\end{displaymath}](img79.gif)
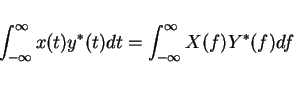
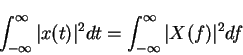
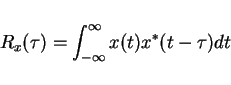
(There are others comparable definition) then
![\begin{displaymath}\underbrace{F}_{w.r.t.\tau}[R_x(\tau]=\vert X(f)\vert^2
\end{displaymath}](img85.gif)
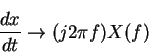
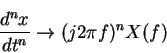
Likewise,
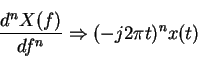
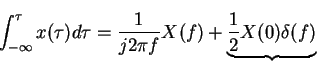
Note that if x(t) has no DC component then this disappears
(will be useful for probability functions)
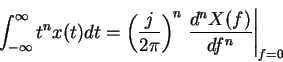
from differentiation theorem
(might want to memorize them)
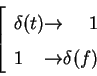
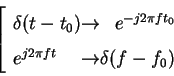
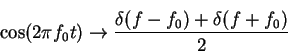
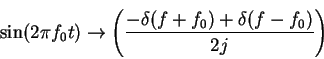
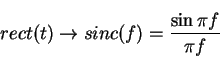
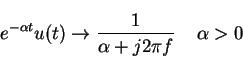
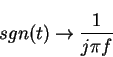
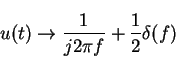
(from integration theorem)
Qualitative
![]() energy concentrated at harmonics
energy concentrated at harmonics
So
x'(t)=x(t+T)
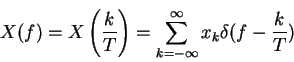
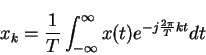
i.e. Fourier series coeff.
![\begin{displaymath}Y(f)=F[\int_{-\infty}^{\infty}x(\tau)h(t-\tau)d\tau]=H(f)Y(f)
\end{displaymath}](img103.gif)
as we used before
If
![]()
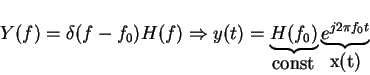
![]() is an EIGENFUNCTION of LTI systems
is an EIGENFUNCTION of LTI systems
![]() that's why we decompose signals onto
that's why we decompose signals onto
![]()
![]()
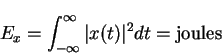
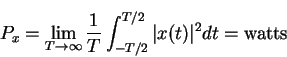
energy signal
![]()
power signal
![]()
or OTHER signals (don't really care
for this designation, but it's analytically useful sometimes)
![\begin{eqnarray*}R_x(\tau) &\equiv& x(\tau)\ast x^*(-\tau)\\
&=&\int_{-\infty}^...
...au)x^*(t)dt\\
& \stackrel{F[]}{\Rightarrow}& \vert X(f)\vert^2
\end{eqnarray*}](img113.gif)
since
rough units: F[joules(t)]
![]() joules.sec=joules/(1/sec)=joules/Hz
joules.sec=joules/(1/sec)=joules/Hz
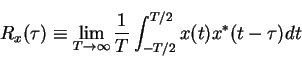
define
![\begin{eqnarray*}S_X(f)&\equiv& PSD (\mbox{\qquad power spectral density})\\
&=&F[R_x(\tau)]
\end{eqnarray*}](img120.gif)
as with energy signals
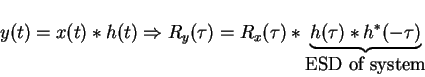
so
Periodic signals are power signals
x(t) periodic,
![]()