Limit in the Mean Convergence

Suppose we have a stochastic process X(t). Assume it's zero mean has correlation function R_X(t₁,t₂)= [X(t₁)X(t₂)]. What we'd LIKE is to be able to represent X(t) as a superposition of orthonormal basis functions, scaled by independent random variables. The independence is a long shot. So what we'll DO is settle for uncorrelated projections on to the orthonormal basis functions.

So, we define $X_N(t) = \sum_{n=1}^N a_n \phi_n(t)$ with $a_n = \int \phi_n(t) X(t) dt$ on some interval and require the following:

$$\lim_{N\rightarrow \infty} E[ (X_N(t) - X(t))^2] = 0$$

That is, we require that X_N(t) converge to X(t) in the mean square sense on the interval of interest.

Note however, that we SEEM to have presupposed that any old set of $\phi_n(t)$ will do. NOT! (in general). We require $E[a_i a_j] = \lambda_i \delta_{ij}$; that is, the a_i are uncorrelated and have variances $\lambda_i$(remember, that X(t) is zero mean therefore so are the a_i).

$$E[a_i a_j] = \int \int X(t)\phi_i(t) X(\tau) \phi_j(\tau) dt d\tau = \int \int R_X(t,\tau)\phi_i(t)\phi_j(\tau) dt d\tau$$

Now remember that we want the $\phi_i$ to be mutually orthonormal AND we would also like them to SPAN the function space on the interval in question (I've left off the limits for generality, but we are talking about a finite interval). We first rewrite the equation

$$\lambda_i \delta_{ij} = E[a_i a_j] = \int \left ( \int R_X(t,\tau)\phi_j(\tau) d\tau \right ) \phi_i(t) dt$$

and we see that we must have

$$\left ( \int R_X(t,\tau)\phi_j(\tau) d\tau \right ) = \lambda_j \phi_j(t)$$

which is a standard integral equation. This form is VERY VERY important. Become intimate with it. We call the $\lambda_i$ eigenvalues of the random process X(t) and likewise the $\phi_i(t)$ are the corresponding eigenfunctions. The analogy to linear algebraic concepts is almost exact. We do, however, require that R_x() be square integrable since if not, we have unbounded variances and all hell breaks loose (in a mathematical sense).

Please also note that had the process not been zero mean, we could have defined the integral equation in terms of the covariance function E[(X(t₁)-m_X(t₁))(X(t₂)-m_X(t₂))] with the same result. However, since carrying the mean around often means (no pun intended) a headache, we assume ``centered'' random variables.

Here are some interesting factoids which we list without proof for the most part:

• $E[\vert a_n\vert^2] = \lambda_n$ is the expected energy projected onto basis function (also called a coordinate... working our way toward signal space) $\phi_n(t)$.
• If R_X(t₁,t₂) is ``positive definite'' all the eigenvalues $\lambda_i$ are greater than or equal to zero. Why don't you now prove that R<sub>X</sub>(t<sub>1</sub>,t<sub>2</sub>) is at least positive ``semi-definite''. What is the definitiion you ask? Well a KERNEL is positive semi-definite if
  
  $$\int \int g(\tau) K(t,\tau) g(t) dt d\tau \ge 0$$
  
  
  for all possible functions g(t). Positive definite means we have a strict inequality. Once again this is analogous to linear algebraic concepts. Just in case you're glazed at this point, remember that $K(t,\tau) = E[ (X(t) - m_X(t))(X(\tau) - m_X(\tau))]$ and that $K_X(t,\tau) = R_X(t,\tau) - m_X(t)m_X(tau)$.
• There's always at least one square-integrable function $\phi(t)$ and real eigenvalue which satisfies the above integral equation.
• If two eigenfunctions have the same eigenvalue, then any linear superposition of the two functions is also an eigenfunction (with the same eigenvalue).
• Eigenfunctions corresponding to different eigenvalues are orthonormal.
• This is at most a countably infinite set of eigenvalues and all are bounded.
• For a given eigenvalue, the number of (linearly independent) associated eigenfunctions is FINITE!
• We can write
  
  $$R_X(t,\tau) = \sum_{i=1}^{\infty} \lambda_i \phi_i(t)\phi_i(\tau)$$
  
  
  This frighteningly useful and ubiquitous relation is called Mercer's theorem.
• If the kernel is positive DEFINITE then we end up with a COMPLETE set of orthonormal functions $\phi_i(t)$ which span the function space on the interval of interest. Because of the square integrability requirement, we can only represent signals with finite energy.
• As you might expect, the energy in the random process is $\sum_i \lambda_i$.

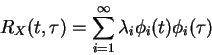
I'll continue this later, but want to get it out. Be wary of typos above. I'll provide the two examples we did in class in what follows.